Measures of Variation
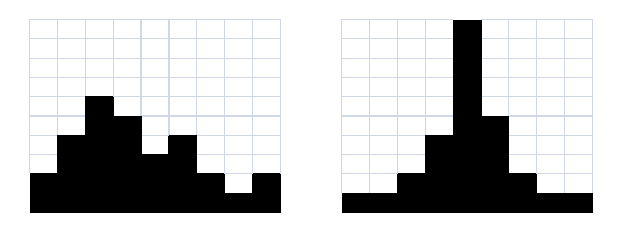
The idea is to measure how widely scattered is a set of data. Consider the two histograms below

The Range
The range is the highest value minus the lowest value. For example for 4, 6, -5, 4, 1, 2 the range is 6 - (-5) = 11. Knowing the range can be helpful, but it is not that useful.
Compare the two histograms above, they each have the same width, so the ranges are the same, and the same number of squares are shaded in each so they contain the same amount of data. The one on the left appears more spread out or more variable. The standard deviation described below turns out to be the most useful way to measure variation.
Variance and Standard Deviation

In practice we do not use this formula to compute the variance. It is intended to help you understand the concept. If data is widely scattered the difference between data values and the mean will be large making the variance large. If data is close together the difference between data values and the mean will be small making the variance small.

A better way to compute the variance is using an equivalent formula, which on the surface seems more complicated, but it avoids having to use the mean, which is helpful when the mean is a complicated decimal.
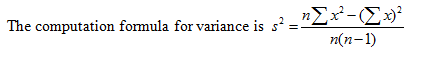
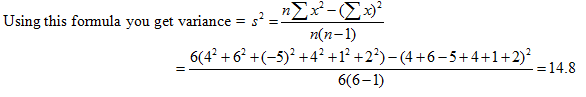

Note a statistic is a measure you get from a sample, such as the variance. A parameter is the corresponding measure for the population. In statistics we use statistics gathered from data to estimate parameters.
Why divide by n - 1 rather than n when computing variances for samples?
The standard deviation is the square root of the variance, denoted s for samples and σ for populations.
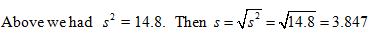
Chebyshev's Rule
It turns out to be useful to measure how far a data value is from the mean in terms of standard deviations for example we say
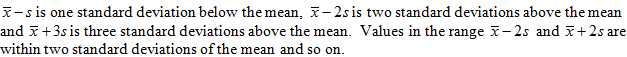
Chebyshev's rule states the following:

For example, a sample of 80 values has mean = 50 and standard deviation = 10. Then at least 60 (= 75% of 80) of the values will lie in the interval 50 - 2(10) to 50 + 2(10), or 30 to 70.
Example: A sample has mean 32 and standard deviation 3. At least what percent of values are guaranteed to lie in the interval 23 to 41?
Answer: In order to be successful in this type of problem you will first need to recognize it is a Chebyshev's rule problem. Having done that you need to see that 23 to 41 is x - 3s to x + 3s
so 88.9% of values lie in the interval 23 to 41.
The Empirical Rule
In nature many distributions turn out to be symmetric and bell-shaped like so
If you have a bell-shaped distribution then the empirical rule applies. It states (Note the approximately as compared to at least in Chebyshev's rule!)
Approximately 68% of values lie in the interval x - s to x + s
Approximately 95% of values lie in the interval x - 2s to x + 2s
Approximately 99.7% of values lie in the interval x - 3s to x + 3s
For example: Batteries have a life that is bell-shaped with a mean life of 72 hours with a standard deviation of 14 hours. What percent of batteries would you expect to last more than 86 hours?
Answer: You first have to recognize that 86 is x + s. You then have a picture
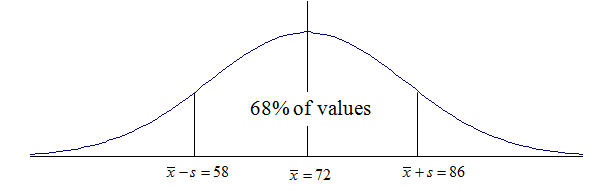
Since the distribution is symmetric the mean is in the middle. There are 68% of values between 58 and 86. There are 32% of values remaining, half of which must be more than 86 and half of which must be less than 58.
You conclude about 16% of batteries will last more than 86 hours.
The Rule of Thumb
The rule of thumb is intended to give you a rough idea what the standard deviation should be. You most likely will not find it a very convincing rule!
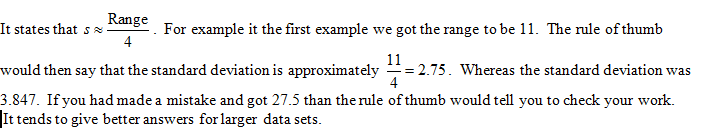
The Coefficient of Variation
Suppose you have two sets of data and you wish to determine which is more variable. The actual size of the variation can depend on how the data is measured. The coefficient of variation can be used to compare two standard deviations. It is defined to be

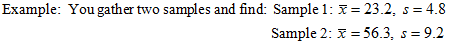
Using the coefficient of variation, which sample is more variable?
You calculate :
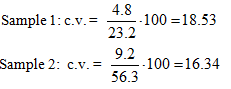
You conclude Sample 1 is more variable.